PRIMERA SEMANA:
GEOMETRÍA ANALÍLTICA EN EL ESPACIO
La recta en R3
- Ecuación vectorial.
Una recta r viene determinada bien por dos
puntos A, B, o bien por un punto A y su dirección (que viene expresada en
forma de un vector director  que es paralelo a r - o en otras palabras- nos indica la dirección de r)
que es paralelo a r - o en otras palabras- nos indica la dirección de r)

Si P es un punto genérico de la recta r (ver
figura 2) se tiene que:
siendo l un cierto
parámetro, y si ahora (fijándonos en la figura 1) tenemos en cuenta
que:
se tiene:
y si consideramos al segmento  como el vector
como el vector  (para ello se opera
así: coordenadas de B menos coordenadas
de A) tenemos:
(para ello se opera
así: coordenadas de B menos coordenadas
de A) tenemos:
Cualquiera de ellas {1}
ó {2} es la ecuación
vectorial de la recta r.
- Ecuaciones paramétricas de la recta .
Sean conocidos dos puntos  de una cierta recta r, entonces podemos tomar como vector director
de una cierta recta r, entonces podemos tomar como vector director
 de esta recta:
de esta recta:  ,
y sea un punto genérico de la recta r, que viene
dado por P(x, y, z)
,
y sea un punto genérico de la recta r, que viene
dado por P(x, y, z)
Entonces la ecuación de la
recta (según {2}) podrá ser expresada:
{3}

que son las llamadas ecuaciones
paramétricas de la recta.
-Ecuación cartesiana de la recta .
Despejemos l
de cada una de las ecuaciones {3}
e igualemos:
Es la llamada ecuación continua de la recta que pasa por dos puntos  .
.
SEGUNDA SEMANA:
El plano en R3
- Ecuación vectorial.
Dados tres puntos no alineados:  ,
forman un plano, y cualquier punto P(x,y,z) de este plano podrá ser expresado en la
forma:
,
forman un plano, y cualquier punto P(x,y,z) de este plano podrá ser expresado en la
forma:
 {5}
{5}
lo cual representa la ecuación
vectorial del plano.
- Ecuaciones paramétricas
del plano.
Si expresamos {5}
en coordenadas tenemos:
{6} 

que son las ecuaciones paramétricas del plano.
- Ecuación cartesiana del plano.
Según hemos visto en el producto mixto de vectores, éste es nulo para el caso de tres vectores
coplanares tales como  (vease figura superior),
por tanto se tiene:
(vease figura superior),
por tanto se tiene:
 {7}
{7}
una ecuación que se reduce a la simple expresión:
a x + b y + c z + d =
0 {8}
 La
particularidad de {8} es
que los tres coeficientes: a, b, c son las
componentes del llamado "vector normal" del plano, tal como se
aprecia en la gráfica de la izquierda.
La
particularidad de {8} es
que los tres coeficientes: a, b, c son las
componentes del llamado "vector normal" del plano, tal como se
aprecia en la gráfica de la izquierda.
Un vector normal al plano es un vector
"perpendicular" a cualquier recta del plano. Así, un plano viene
determinado por un vector normal n (a, b, c) y un punto A.
Por ejemplo: El plano cuyo vector normal es n
(1, 3, -1) y que pasa por el punto A(2,0,5) es:
1. x + 3. y + (-1) . z + d = 0
x + 3y - z + d = 0
y si ahora sustituimos el punto A(2,0,5):
2 + 3.0 - 5 + d = 0
de donde sacamos que d = -3. Por lo tanto, ese plano
en coordenadas cartesianas es:
x + 3y - z - 3 = 0
- Ecuación de la recta como intersección de dos planos
Hasta ahora hemos visto la ecuación de una recta en
coordenadas paramétricas y en cartesianas. Ahora vamos a ver también que
dados dos planos que se intersectan definen una recta (tal como se aprecia en la figura de la derecha).
definen una recta (tal como se aprecia en la figura de la derecha).
 definen una recta (tal como se aprecia en la figura de la derecha).
definen una recta (tal como se aprecia en la figura de la derecha).
Entonces una pareja de dos planos define una
recta:
{9} 

* Haz de planos
Dada una pareja de planos que se intersectan, tal
como la {9}, hay otros infinitos
planos que también se intersectan en esta recta, a todos ellos se les
denomina "haz de planos", su ecuación general es:
-Ecuación del plano que pasa por tres puntos.
Dados tres puntos no alineados en el espacio,  definen un plano, cuya ecuación viene dada por:
definen un plano, cuya ecuación viene dada por:
 {11}
{11}- Posición entre recta y plano.
1)  Para
que una recta, con vector director
Para
que una recta, con vector director  ,
y un plano con vector normal
,
y un plano con vector normal  ,
sean paralelos , se debe cumplir que estos dos vectores sean perpendiculares:
,
sean paralelos , se debe cumplir que estos dos vectores sean perpendiculares:  .
.
 Para
que una recta, con vector director
Para
que una recta, con vector director
Es decir, se debe cumplir que:  {12}
{12}
Un ejemplo:
2) Para
que una recta, con vector director  ,
y un plano con vector normal
,
y un plano con vector normal  ,
,
 sean perpendiculares , se
debe cumplir que estos dos vectores sean paralelos
sean perpendiculares , se
debe cumplir que estos dos vectores sean paralelos
 sean perpendiculares , se
debe cumplir que estos dos vectores sean paralelos
sean perpendiculares , se
debe cumplir que estos dos vectores sean paralelos
En este caso, la condición que se deberá verificar
es que ambos vectores sean proporcionales, es decir:
-Sobre ángulos.
* Ángulo entre dos rectas:
Sean dos rectas, con vectores directores  ,
el ángulo formado por estas dos rectas viene dado por:
,
el ángulo formado por estas dos rectas viene dado por:
* Ángulo entre dos planos:
Sean dos planos: 

 El
ángulo formado por los dos planos coincide con el que forman su vectores
normales respectivos (según el lema de "igualdad de ángulos entre rectas
perpendiculares")
El
ángulo formado por los dos planos coincide con el que forman su vectores
normales respectivos (según el lema de "igualdad de ángulos entre rectas
perpendiculares")
Por lo tanto, se tiene:

Esfera
Ecuación cartesiana
En un sistema de coordenadas cartesianas en un espacio euclidiano tridimensional, la ecuación de la esfera de radio 1, con centro en el origen, es:Esta ecuación se obtiene considerando que en el punto M (x, y, z) de la esfera, el vector normal OM es igual a 1.
Generalizando, la esfera de radio r, de centro Ω (a, b, c) tiene como ecuación:
TERCERA SEMANA:
ANÁLISIS DE SUPERFICES EN EL ESPACIO
Elipsoide
La ecuación implícita del elipsoide centrado enLa representación que vemos a la derecha corresponde al elipsoide de centro
Para representar el elipsoide con centro
1. Las intersecciones con los ejes coordenados
-ox
-oy
-oz
2. Las intersecciones con los planos
-xoy
-xoz
-yoz
3. Las intersecciones con los planos paralelos a los planos principales
-xoy
-xoz
-yoz
CUARTA SEMANA:
FUNCIONES VECTORIALES
En la ciencia y la ingeniería a menudo es conveniente introducir un vector r con las funciones f y g como componentes.
R(t) = < f(t), g(t)> =f(t)i + g(t)j
Se dice que r es una función vectorial. De manera semejante, una curva en el espacio es parametrizada por 3 ecuaciones
X = f(t) y = g(t) z = h(t) a " t " b
Una función vectorial se expresa como:
R(t) = < f(t),g(t), h(t) > = f(t) I +g(t) j + h(t)k
Cuando t varia es posible imaginar que la curva C esta siendo trazada por la punta móvil de r(t)
Limites y continuidad
La función fundamental de limite de una función vectorial se define en términos de los limites de las funciones componentes
Lim r(t) = lim f(t), lim g(t), lim h(t)
TEOREMA
Si lim t a r1(t) = L1 y lim t a r2 (t) = L2 entonces
Lim C r1 (t) = CL1, C en donde C es un escalar
(ii) lim [ r1 + r2 (t) = L1 + L2
lim r1 . rt2 = L1 . L2
Derivadas de funciones vectoriales
La derivada de una función vectorial r e:
r'(t) = lim 1/ t [r (t + t) - r(t)]
TEOREMA
Si r(t)= ( f(t), g(t), h(t) ), en donde f,g,h son diferenciables, entonces
r'(t) =( f'(t). g'(t).h'(t) )
Interpretación geométrica de r'(t)
Si el vector r't no es 0 en un punto p, entonces puede dibujarse tangente a la curva en p.
r = r(t + t) - r(t)
r/ t = 1/ t [r (t + t)-r(t)
Movimiento sobre una curva
Velocidad y aceleración
Supóngase
que un cuerpo o una partícula móvil describe una trayectoria C, y que
su posición en ella esta dada por la función vectorial
R(t) = f(t)i + g(t)j +h(t)k
En donde t representa el tiempo. Si f, g y h tienen segundas derivadas, entonces los vectores
V(t) = r'(t)= f'(t) + g'(t)j + h'(t)k
a(t) =r''(t) =f''(t)i + g''(t)j + h''(t)k
se llaman velocidad y aceleración de la partícula, respectivamente. La
función escalar øv(t)ø= ødr/dtø ="(dx/dt)2+ (dy/dt)2+dz/dt)2
la longitud esta relacionada con la longitud de arco s mediante s'(t) =øv(t)ø
s = " øv(t)ø dt
QUINTA SEMANA
TRIEDRO MÒVIL
Definición
Sea T ⊂ R3 una curva y sean γ : I = [a, b] → R3, γ(t) = (x(t), y(t), z(t)) una
parametrización regular y α : I′ = [a′, b′] → R3 su parametrización respecto el
parámetro arco.
A partir de la primera y segunda derivada de la parametrización de la curva
se construye el triedro de Frenet. En cada punto regular de la curva γ(t), son
tres vectores unitarios y ortonormales, T(t), B(t) y N(t). Es decir, el triedro de
Frenet es un sistema de referencia ortonormal que nos proporciona
información sobre la curva. Decimos que es un sistema de referencia móvil,
porque se desplaza por la curva según la recorremos.
parametrización regular y α : I′ = [a′, b′] → R3 su parametrización respecto el
parámetro arco.
A partir de la primera y segunda derivada de la parametrización de la curva
se construye el triedro de Frenet. En cada punto regular de la curva γ(t), son
tres vectores unitarios y ortonormales, T(t), B(t) y N(t). Es decir, el triedro de
Frenet es un sistema de referencia ortonormal que nos proporciona
información sobre la curva. Decimos que es un sistema de referencia móvil,
porque se desplaza por la curva según la recorremos.

A partir de los vectores del triedro de Frenet construiremos planos (el osculador, el normal y el rectificante). También introduciremos los conceptos de curvatura y torsión, que nos darán información de cómo se “dobla” y “retuerce” la curva en el espacio.
Para llegar calcular el Triedro de Frenet en cualquier punto de una curva, lo primero que debemos hacer es parametrizarla (en el caso de que no lo este). Una vez que hallamos parametrizado la curva en cuestión, generalmente mediante coordenadas polares, podemos comenzar a “construir” nuestro Triedro de Frenet.
Para llegar calcular el Triedro de Frenet en cualquier punto de una curva, lo primero que debemos hacer es parametrizarla (en el caso de que no lo este). Una vez que hallamos parametrizado la curva en cuestión, generalmente mediante coordenadas polares, podemos comenzar a “construir” nuestro Triedro de Frenet.
Vector Tangente.
Lo primero que deberíamos hacer es calcular el vector Tangente del triedro, ya que sobre él están basadas todos los cálculos posteriores. Para calcularlo utilizaremos la siguiente fórmula:
*Donde r (t) es el vector que define a nuestra curva ya parametrizada, r’(t) es su derivada y |r’(t)| es el módulo de la derivada.
Vector Normal Principal.
En segundo lugar debemos calcular el vector Normal Principal del triedro, para hallar su expresión usaremos esta fórmula:
*Donde T’ (t) es la derivada del vector Tangente y | T’ (t) | es el módulo de la derivada.
Vector Binormal.
En último lugar para completar el Triedro de Frenet, tenemos la necesidad de hallar cual es el vector Binormal, el cual es normal al Vector Tangente y al Vector Normal Principal, de ahí que podamos calcularlo mediante un simple producto vectorial entre ambos vectores:
B = T x N
Longitud de la curva.
Otro apartado importante, que se ve junto con el Triedro de Frenet, es como poder llegar a calcular la longitud de la curva con la que estamos trabajando.
Generalmente, usaremos la siguiente expresión:
Generalmente, usaremos la siguiente expresión:
Sin embargo, un muchas ocasiones esta integral no posee una primitiva con la cual calcular el valor de L, por lo que deberemos usar Métodos de Integración Numérica para poder aproximar el valor de L. Todos estos métodos suelen dar valores muy cercanos al verdadero, con errores inferiores al 5%.
Uno de los métodos que, personalmente, recomiendo es La Regla del Trapecio, debido principalmente a la facilidad de su uso y de su recordatorio. La cual es la siguiente:
Uno de los métodos que, personalmente, recomiendo es La Regla del Trapecio, debido principalmente a la facilidad de su uso y de su recordatorio. La cual es la siguiente:
Otros métodos de integración numérica son estos:
Curvatura y Torsión.
Otra de las cosas que veremos en este apartado de la asignatura de Cálculo II, es la curvatura, así como el radio de curvatura, y también la torsión, todas ellas características propias de la curva que estamos estudiando.
Curvatura, radio de curvatura y círculo osculador.
La curvatura es una medida del cambio de dirección del vector tangente a una curva, cuanto más rápido cambia éste a medida que nos desplazamos a lo largo de la curva, se dice, que más grande es la curvatura. Su expresión es:
De esta misma manera, definimos el radio de curvatura como la magnitud que mide la curvatura de un objeto geométrico, tal como una línea curva, una superficie o ,más en general, una variedad diferenciable definida en un espacio euclídeo. Su expresión es:
En este apartado, además veremos el círculo osculador, que por así decirlo es el que “besa” a la curva en un punto dado. Una definición un poco más técnica sería esta: es una circunferencia cuyo centro se encuentra sobre la normal a la curva y tiene la misma curvatura que la curva dada en ese punto. El centro y el radio de la circunferencia osculatriz, en un punto de la curva, son llamados centro de curvatura y radio de curvatura de la curva en ese punto. El plano en el que está contenida la circunferecia osculatriz se denomina plano osculador.
 *Donde el radio de curvatura es ρ.
*Donde el radio de curvatura es ρ.6.2. Torsión.
La torsión es una medida del cambio de dirección del vector binormal: cuanto más rápido cambia la torsión, más rápido gira el vector binormal alrededor del vector tangente y más retorcida aparece la curva. Por lo tanto, para una curva totalmente contenida en el plano, la torsión es nula, ya que, el vector binormal es constantemente perpendicular al plano que la contiene. Su expresión es:

Planos del Triedro de Frenet.
Por último, en este apartado de la asignatura, debemos aprender a calcular y a dominar los conceptos de plano Normal, Rectificante y Osculador.

Como podemos ver en la imagen el Plano Normal es perpendicular al Vector Tangente, el Plano Rectificante es perpendicular al Vector Normal Principal y el Plano Osculador es normal al Vector Binormal. Sus expresiones son:
Plano Normal.
(X−r(t))∗T=0
Plano Rectificante.
(X−r(t))∗N=0
Plano Osculador.
(X−r(t))∗B=0


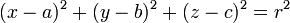

Este comentario ha sido eliminado por el autor.
ResponderEliminar